 堆
堆
# 堆
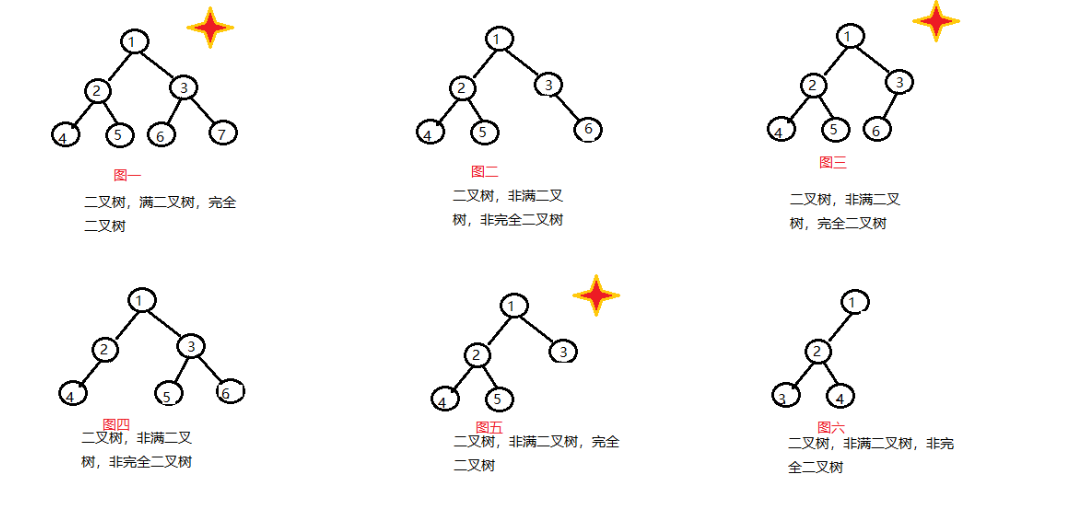
完全二叉树的定义仅为个人理解:除了最底层可以是不满的,其他层必须都是满的,底层节点不满的时候,底层节点必须是连在一起的
打个比方:图二 就是底层节点不满的情况,节点4,5与节点6之间就断开了。其要变成完全二叉树要么把6删除,要么在4,5,与6之间加一个加点,也就是3节点的左子树。
heap 其实是一个抽象的数据结构,或者说是逻辑上的数据结构,并不是一个物理上真实存在的数据结构。简单点说就是,堆并没有其对应的实际的物理数据结构,像数组,链表,二叉树等都有自己对应的物理层面的数据结构,而堆只是一个逻辑上的数据结构,该数据结构有着特定功能。
堆的实现有多种,主要的目的就是要实现堆这种数据结构的功能,也就是实现优先级队列,**要能够动态的将放入堆的数据按照优先级进行排序,注意是动态的,**不是说像存在一个普通数组一样,每加一个数据就重新排一次序,这样效率太低,优先级队列是能够在添加,删除的过程中动态的维护优先级。
此处介绍二叉堆
二叉堆
标准定义上,我们认为一颗树满足以下的两点,就是一个堆,
- 一颗完全二叉树
- 每个节点的值大于等于(或小于等于)其子树中每个节点的值
根据子节点与父节点值的大小关系,可以把堆分为,
- 最大堆 (opens new window)(也叫大根堆,大顶堆),任意父节点都比其子节点的值要大
- 最小堆 (opens new window)(也叫小根堆,小顶堆),任意父节点都比其子节点的值要小
在二叉堆的实现上实际上是使用数组来实现的
树的存储方式一般有链式存储和线性存储,分别对应我们常见的链表和数组两种方式,对于完全二叉树而言,用数组来存储是非常节省存储空间的,因为不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点,
实现可参考
https://labuladong.gitee.io/algo/data-structure/binary-heap-priority-queue/#%E4%BA%8C%E3%80%81%E4%BC%98%E5%85%88%E7%BA%A7%E9%98%9F%E5%88%97%E6%A6%82%E8%A7%88
