常见排序算法

冒泡

 /**
     * 冒泡排序                时间复杂度
     */
    public static void sort1(int[] nums) {

        for (int i = 0; i < nums.length - 1; i++) {
            for (int j = 0; j < nums.length - i - 1; j++) {
                if (nums[j] > nums[j + 1]) {
                    int vb = nums[j];
                    nums[j] = nums[j + 1];
                    nums[j + 1] = vb;
                }
            }
        }
    }

选择

/**
     * 选择排序             时间复杂度
     */

    public static void sort2(int[] nums) {

        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] > nums[j]) {
                    int vb = nums[i];
                    nums[i] = nums[j];
                    nums[j] = vb;
                }
            }
        }
    }

快速

    /**
     *   快速排序          时间复杂度
     */

    public static void sort3(int[] nums,int left,int rigth) {
          if(left >= rigth){
              return;
          }
        int partition = partition(nums, left, rigth);
          sort3(nums,left,partition-1);
          sort3(nums,partition+1,rigth);
    }

    public static int partition(int[] nums,int left,int right){
       int pivot = nums[right];
       int index = left;

       for(int i=left;i<right;i++){
        if(nums[i]< pivot){
          swap(nums,i,index);
          index++;
        }
       }
       swap(nums,index,right);
       return index;
    }

    public static void   swap(int [] nums,int i,int j){
         int jk = nums[i];
         nums[i] = nums[j];
         nums[j] = jk;
    }

插入

/**
     * 插入排序            时间复杂度
     */

    public static void sort4(int[] nums) {

        for(int i=1;i<nums.length;i++){

            int t = nums[i];
            int j = i-1;
            while(j>=0){
                if(nums[j]>t){
                    nums[j+1] = nums[j];
                }else {
                    break;
                }
                j--;
            }
            nums[j+1] = t;
        }
    }

排序算法的稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

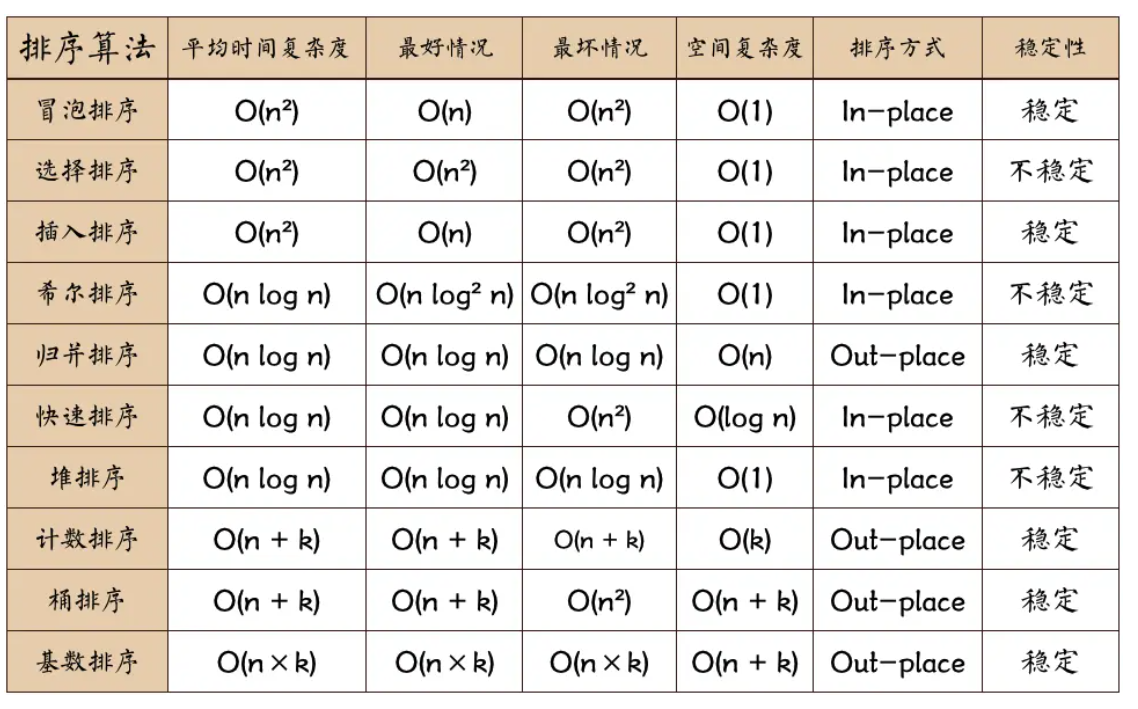
排序算法稳定性的意义

• 如果只是简单的进行数字的排序，那么稳定性将毫无意义。
• 如果排序的内容仅仅是一个复杂对象的某一个数字属性，那么稳定性依旧将毫无意义
• 如果要排序的内容是一个复杂对象的多个数字属性，但是其原本的初始顺序毫无意义，那么稳定性依旧将毫无意义。
• 除非要排序的内容是一个复杂对象的多个数字属性，且其原本的初始顺序存在意义，那么我们需要在二次排序的基础上保持原有排序的意义，才需要使用到稳定性的算法，例如要排序的内容是一组原本按照价格高低排序的对象，如今需要按照销量高低排序，使用稳定性算法，可以使得想同销量的对象依旧保持着价格高低的排序展现，只有销量不同的才会重新排序。（当然，如果需求不需要保持初始的排序意义，那么使用稳定性算法依旧将毫无意义）。

在实际应用中，我们面对的数据对象往往都是复杂的，每个对象可能具有多个数字属性且每个数字属性的排序都是有意义的。所以在排序时，我们需要关注每个数字属性的排序是否会对其他属性进行干扰。

举个例子，假如我们要给大学中的学生进行一个排序。每个学生都有两个数字属性，一个是学生所在年级，另一个是学生的年龄，最终我们希望按照学生年龄大小进行排序。而对于年龄相同的同学，我们希望按照年级从低到高的顺序排序。那么要满足这样的需求，我们应该怎么做呢？

如果我们利用具有稳定性的排序算法，这个问题就会更好地解决了。我们先按照年级对学生进行排序，然后利用稳定的排序算法，按年龄进行排序。这样，只需要运用两次排序，我们就完成了我们的目的。这是因为，稳定的排序算法能够保证在排序过程中，相同年龄的同学，在排序之后，他们的顺序不发生改变。由于第一次我们已经将学生按年级排序好了，于是在第二次排序时，我们运用稳定的排序算法，相同年龄的学生依旧按年级保持顺序。

可以看出排序算法的稳定性是在我们面对复杂对象的排序时，需要按照对象的多个属性进行排序，后面属性的排序不能改变前面属性排序元素中相同元素的相对位置（当前属性排序认为的相同），即A元素与B元素被认为是相同的，A在B之前，排序之后， A与B的相对位置没有发生改变。以上面的例子举例就是，在年龄相同的条件下，按年级排序，具体步骤就是

• 先按年级排序，此处不需要稳定排序
• 按年龄排序，此处需要稳定排序，效果就是当多个年龄相同时候每个年龄相同的元素的相对位置没有发生改变，也就是说，是按照年级排序好的，在年龄相同的条件下，按年级排序

Java 提供的常见排序API

Arrays.sort(T[],Comparator<? super T> c) 内部采用的归并排序，因此是稳定的。

Arrays.sort(int[] a) 内部采用的快速排序，因此是不稳定的。

Collections.sort(List list)、和Collections.sort(List list，Comparator<？super T> c); 采用的都是稳定的排序，采用的何种排序方式，需要核实。