算法刷题思想

去重

哈希保存元素状态法

通过哈希表存储已经出现过的元素

双指针

先排序，再基于排序的基础上按照具体情况进行去重 如三数之和，以及回溯中需要去重的题

递归

对于递归算法，最重要的就是明确递归函数的定义，不要跳进递归（你的脑袋能压几个栈呀？），而是要根据刚才的函数定义，来弄清楚这段代码会产生什么结果：主要是根据具体的处理代码来判断。也就是说，单个节点的处理代码就是该递归函数的意义

往下的过程就是递，再从下返回上的过程就是归

在向下的过程中把问题解决，还是在回退的过程中把问题解决，注意与回溯的联系，进行对比

快速排序 反转链表 全排列

基本就是处理逻辑是在递归代码前还是后

无返回值的

在递的过程中解决问题

处理逻辑是在递归代码之前的，也就是说，他不需要自己下层的递归函数有任何返回值来帮助进行程序的运行，

解决问题是从上往下解决问题。

有返回值的

在归的过程中解决问题

处理逻辑是在递归代码之后的，也就是说，他需要自己下层的递归函数有任何返回值来帮助进行程序的运行，

解决问题是从下往上执行问题，因为上面的递归函数需要下面的递归函数的返回值来帮助程序运行。

注意

上面举例的无返回值与有返回值，实际上并不准确，因为无返回值也可以在归中解决问题，有返回值也能再递中解决问题，总结就是递归有两种解决方法：从上往下，递中解决，处理逻辑是在递归代码之前。从下往上，归中解决，处理逻辑是在递归代码之后的。 补充： 处理逻辑是在递归代码之前与处理逻辑是在递归代码之后，并不是该两中方法各自的特点，而是都能存在于对方的方法中，如二叉树的遍历实际上关键在于，你想在递归前做些事情就写在递归代码前，想在递归后做些事情就写在递归代码后。

不需要用到返回值来参与代码运行的，终止条件返回什么都行，

int max = 0;
int count =0;
public int maxDepth(TreeNode root) {
    if(root == null){
        return max;   0 ,1 ,2都行
    }
    count++;
    max = max < count ? count:max;
    maxDepth(root.left);
    maxDepth(root.right);
    count--;

    return max;
}

一般来说，在递的过程中处理节点的是不需要使用返回值的，反之

回溯

去重问题

先排序

去重是判断是否在同一层使用过，对应到代码是本次for循环当中的元素。下一层不管：所谓下一层，就是递归向下的下一层。for循环横向遍历（同一层），递归纵向向下到下一层。

for循环内的代码都是本层的逻辑

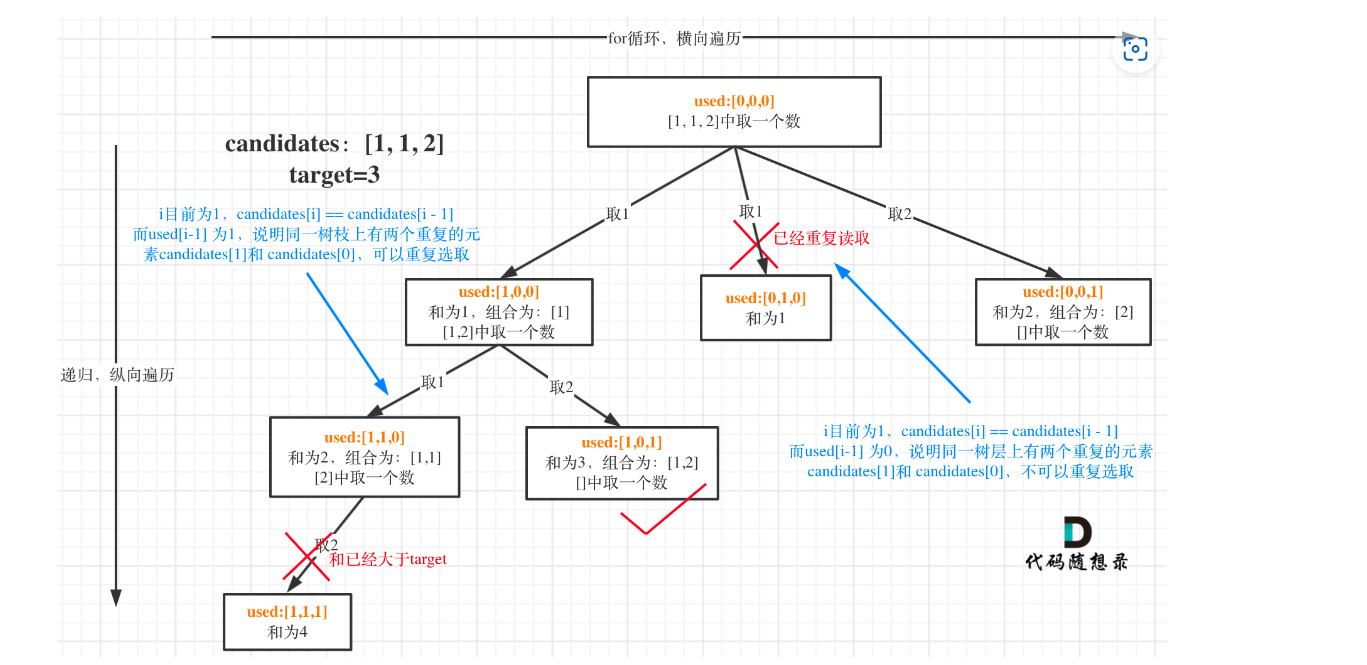
组合与排列的去重逻辑都一样

一定要先排序

if(i!=0 && nums[i] == nums[i-1] && !used[i-1]){
    continue;
}

used的判断是会出现 589936 9是i 9 是i-1 此时i-1是下一层的，不是与i一层的，及时一样也不算重复

链表

反转

递归魔法：反转单链表 | labuladong 的算法笔记 (gitee.io) (opens new window)

反转整个引申到反转前n个再引申到反转链表的指定局部， 递归法

环形

哈希法

快慢指针， fast为slow的两倍速，相遇就是有环，若需进一步得出环的起始节点。快慢指针，相遇后，启一个新的head节点与slow同时遍历，直到相等，就是起始点

删除链表

删除 也需要用到双指针

需要自己添加一个虚拟头指针，两个指针一前一后。

动态规划

先找到问题存在的递推关系，接着就根据找到的递推关系确定dp数组的含义，初始化，写出递推公式，然后采用合适的遍历顺序解决问题。

动态规划的结果就是在dp数组中根据递推关系和dp数组里的开始的几个用于递推的初始值从而地推出dp数组中所有元素的值

递推公式就是非特殊的处理方式，加上特殊的处理方式，请看下面例子

dp i，j = true 条件 s[i] == s[j] && j-i<=1 ---特殊情况，较少的几个元素点是这个规则

dp[i] [j] = true 条件 s[i] == s[j] &&dp[i + 1] [j - 1] ==true ---非特殊情况 大多数元素的遵循该规则

也就是说找的递推关系是可以使用的也是正确的，但是需要排除几个单独的元素点。

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

dp数组就是根据找到的递推关系确定意义的，再根据递推关系写出递推公式和，逻辑代码。

遍历顺序最本质的一点：遍历的顺序需要满足递推关系中对于递推所需要使用到的dp数组的元素的提供，要是已经确定的，

比如：dp[i] [j] = dp[i+1] [j-1] +1的话，你就必须要保证该递推关系中对于递推所需要使用到的dp数组的元素dp[i+1] [j-1]的提供，要是已经确定的值。 从而遍历顺序就会是i 从下往上，j从左往右。保证dp[i+1] [j-1] 的值是已经递推出结果的。

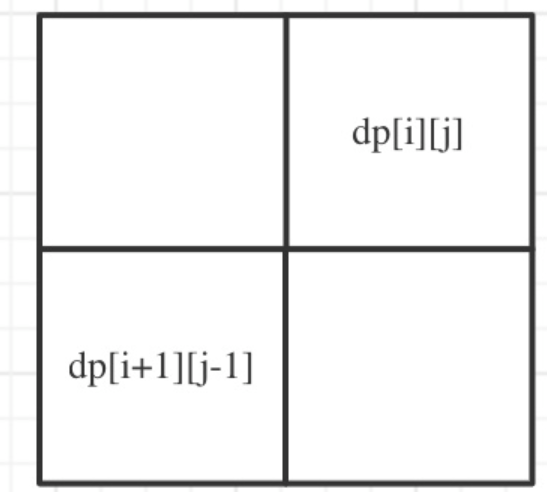
子序列问题

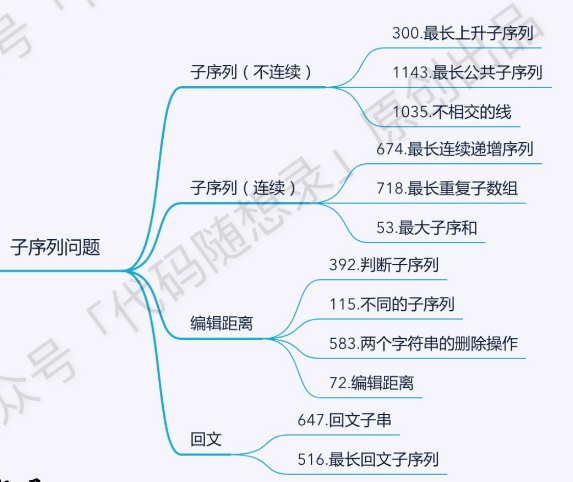
子序列的连续与不连续的处理的上存在区别

本质上就是递推关系的不同，连续时的dp[i] 由dp[i-1] 推导，不连续时的dp[i] 由dp[0]到dp[i-1]的元素推导

二维dp

遍历顺序的根本在于：

二叉树

二叉树的处理离不开二叉树的遍历，一般而言用的是三种：前序（中左右），中序（左中右），后序（左右中）

不管是什么遍历，处理逻辑一定是在中处理的 所以前序相当是从上往下处理，后序是从下往上

没每种遍历都有自己的特性，要根据具体情况使用合适的遍历

排序

快速排序的双指针实现左小右大，类似题在双指针包中